En esta materia te permiten llevar al parcial una hoja de fórmulas, lo cual es un golaaaaaazo 🙌, peeeeero (siempre hay un pero, no? jeje) la contra es que suelen confiarse demasiado en esa hojita y no les prestan atención a al fórmulas😅. Lo malo de esto es que terminás sin entender qué fórmula aplicar y cuándo aplicarla en un ejercicio.
Es por eso que no soy muy fan de dar hojas de fórmulas, siempre voy a preferir que te tomes el momento de hacerte la tuya, porque creo que tomarte el momento para hacerla implica: revisar los temas, repasar en qué momentos se usan, y de paso las vas memorizando (al menos parcialmente).
Pero sí pienso que está bueno tener un lugar donde encontrarlas todas, para poder comparar con tu hoja. Por eso te dejo esta a continuación, con las fórmulas ordenadas por tema👇
📚 CINEMÁTICA
MRU:
$x = x_0 + v \cdot (t - t_0)$ -> Ec. horaria de posición
$v = \dfrac{\Delta x}{\Delta t}$ -> Ec. horaria de velocidad
$a = 0$, $v=cte$
MRUV:
$x = x_0 + v_0 \cdot (t - t_0) + \dfrac{1}{2} \cdot a \cdot (t - t_0)^2$ -> Ec. horaria de posición
$v = v_0 + a \cdot (t - t_0)$ -> Ec. horaria de velocidad
$a = \dfrac{\Delta v}{\Delta t}$
$v_f^2 - v_0^2 = 2 \cdot a \cdot \Delta x$ (Ecuación complementaria⚠️)
⚠️ Consultá si tu docente te deja usarla
Tiro vertical y caída libre son MRUVs que ocurren en el eje $y$, por lo tanto su ecuación horaria de posición es la misma, pero sobre el eje $y$:
$y = y_0 + v_0 \cdot (t - t_0) + \dfrac{1}{2} \cdot a \cdot (t - t_0)^2$ -> Ec. horaria de posición
📚 DINÁMICA
$\sum F_x = m \cdot a_x$ -> Segunda Ley de Newton
$|P| = m \cdot |g|$ -> acordate que el signo de la gravedad queda definido por el SR que vos hayas elegido.
📚 TRABAJO Y ENERGÍA
*Aclaración: Yo a veces uso $W$ y a veces $L$ para referirme a trabajo. Vos usá la que prefieras.
$W_F = |F| \cdot |\Delta x| \cdot \cos(\alpha)$
$E_c = \dfrac{1}{2} \cdot m \cdot v^2$
$E_{pg} = m \cdot g \cdot h$
$E_M = E_c + E_p$
$\Delta E_M = W_{F.N.C.}$ -> Teorema del trabajo de las fuerzas no convervativas y la variación de la energía mecánica
$\Delta E_c = W_{F.\text{resultante}}$ -> Teorema del trabajo de fuerza resultante y la variación de la energía cinética
$- \Delta E_{pg} = W_P$
$\text{Pot}M = \dfrac{W}{\Delta t}$ -> Potencia media
$\text{Pot}{\text{inst}} = |F| \cdot |v| \cdot \cos(\alpha)$ -> Potencia instantánea
___________________
🌊 FLUIDOS
Prensa hidráulica (principio de Pascal):
$P = \dfrac{F}{A}$
$\dfrac{F_1}{A_1} = \dfrac{F_2}{A_2}$
Hidrostática:
$\delta = \dfrac{m}{V}$
$P_{\text{abs}} = P_{\text{atm}} + P_{\text{manométrica}}$
$P_h = \delta \cdot g \cdot h$ -> Teorema General de la hidrostática
$\Delta P_h = \delta \cdot g \cdot \Delta h$ -> Teorema General de la hidrostática (entre dos puntos)
Hidrodinámica:
$Q = \dfrac{V}{\Delta t}$
$Q = S \cdot v$
$S_1 \cdot v_1 = S_2 \cdot v_2$ -> Ecuación de continuidad
$Q_{\text{total}} = S_1 v_1 + S_2 v_2 + \cdots + S_n v_n$
Fluidos ideales (Bernoulli):
$P_A + \dfrac{1}{2} \cdot \delta \cdot v_A^2 + \delta \cdot g \cdot h_A = P_B + \dfrac{1}{2} \cdot \delta \cdot v_B^2 + \delta \cdot g \cdot h_B$ -> Ecuación de Bernoulli
$v = \sqrt{2 \cdot g \cdot h}$ -> Torricelli. No es que tengas que saberla, se deduce de Bernoulli en ciertos ejercicios
Fluidos reales (Poiseuille):
$\Delta P = Q \cdot R_H$ -> Ecuación de Poiseuille
$R_H = \dfrac{8 \cdot \eta \cdot L}{\pi \cdot r^4}$ -> En el video de la Ley de Poiseuille hay otras 2 fórmulas más, equivalentes a ésta. Pero esta es la más común.
Asociación Resistencias:
Resistencias en serie:
$R_T = R_1 + R_2 + \cdots + R_n$
$Q_T = Q_1 = Q_2 = \cdots$
$\Delta P_T = \Delta P_1 + \cdots$
Resistencias en paralelo:
$\dfrac{1}{R_T} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + \cdots$
$Q_T = Q_1 + Q_2 + \cdots$
$\Delta P_T = \Delta P_1 = \cdots$
________________
💨 GASES
$P \cdot V = n \cdot R \cdot T$ -> Ec. de estado de los gases ideales
$X_i = \dfrac{n_i}{n_{\text{total}}}$
$P_T = i \cdot P_i$ -> Ec. de estado de los gases ideales
$P_i = P_T \cdot X_i$ -> Ley de Dalton
________________
📚 MECANISMOS DE TRANSPORTE
Difusión:
Flujo: $\Phi = D \cdot A \cdot \dfrac{|\Delta C|}{|\Delta x|}$ -> unidades de $[\mathrm{mol/s}]$
Densidad de flujo: $\phi = D \cdot \dfrac{|\Delta C|}{|\Delta x|} = P \cdot |\Delta C|$ -> unidades de $[\mathrm{mol/m^2s}]$
Ósmosis:
$\pi = \text{Osmolaridad} \cdot R \cdot T$
$\text{Osmolaridad} = M \cdot i$
______________
🌡️ CALORIMETRÍA
$Q = m \cdot C_e \cdot \Delta T$ -> Calor sensible (cuando hay variación de T)
$Q = m \cdot L$ -> Calor latente (cuando hay cambio de estado de agregación)
$\sum Q = 0$ -> en recipientes adiabáticos
Experiencia de Joule: $W = 2 \cdot |P| \cdot n \cdot h$
Transmisión de calor - Conducción:
$\dfrac{Q}{\Delta t} = k \cdot A \cdot \dfrac{T_{\text{mayor}} - T_{\text{menor}}}{L}$ -> Ley de Fick
______________
🔥 TERMODINÁMICA
1° Ley: $\Delta U = Q - W$
2° Ley: $\Delta S_{\text{univ}} = \Delta S_{\text{sist}} + \Delta S_{\text{ent}} \geq 0$
Evoluciones reversibles de gases ideales:
· $n$ son los moles
· Para gas monoatómico: $c_v = \frac{3}{2} R$ y $c_p = \frac{5}{2} R$
· Para gas diatómico: $c_v = \frac{5}{2} R$ y $c_p = \frac{7}{2} R$
• Evolución isocórica (V = constante):
· $\Delta U = Q = n c_v (T_f - T_0)$
· $Q = = \Delta U = n c_v (T_f - T_0) $
· $L = 0$ -> V cte, el sistema no realiza ni recibe trabajo
· $\Delta S = n c_v \ln \left(\frac{V_f}{V_0}\right)= n c_v \ln \left(\frac{T_f}{T_0}\right)$
• Evolución isobárica (P constante):
· $\Delta U = n c_v (T_f - T_0)$
· $Q = n c_p (T_f - T_0)$
· $\Delta S = n c_p \ln \left(\frac{V_f}{V_0}\right) = n c_p \ln \left(\frac{T_f}{T_0}\right)$
• Evolución isotérmica (T constante):
· $\Delta U = 0$
· $Q = L = n RT \ln \left(\frac{V_f}{V_0}\right)$
· $L = Q = n RT \ln \left(\frac{V_f}{V_0}\right) $
· $\Delta S = \frac{Q}{T}$
• Evolución adiabática
· $\Delta U = n c_v (T_f - T_0)$
· $\Delta S = \frac{Q}{T}$
• Evolución de un CICLO
· $\Delta U = 0$
· $Q = L$
· $L$ -> área encerrada en gráfica P vs V = sumatoria de los L de cada proceso del ciclo $(L_{ciclo} >0)$
· $\Delta S = 0$
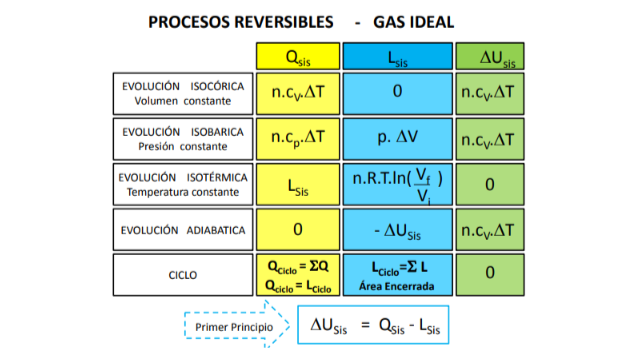
Cuadro resumen de procesos reversibles:
Máquinas térmicas:
$|Q_1| = |Q_2| + W_{\text{neto}}$ -> 1º Ley
$\dfrac{|Q_2|}{T_2} \geq \dfrac{|Q_1|}{T_1}$ -> 2º Ley
$\eta_{\text{real}} = \dfrac{W}{|Q_1|} = 1 - \dfrac{|Q_2|}{|Q_1|}$
$\eta_{\text{ideal o Carnot}} = 1 - \dfrac{T_2}{T_1}$
_____________
⚡ ELECTRICIDAD
Electrostática:
$|F| = \dfrac{k}{\varepsilon_r} \cdot \dfrac{|Q_1| \cdot |Q_2|}{d^2}$ -> Ley de Coulomb. Expresa la fuerza electrostática entre dos cargas puntuales.
$E = \dfrac{F}{q}$ -> Definición de campo eléctrico: es la fuerza que actúa sobre una carga de prueba dividida por el valor de esa carga.
$E = \dfrac{k}{\varepsilon_r} \cdot \dfrac{Q}{d^2}$ -> Campo eléctrico creado por una carga puntual: intensidad del campo eléctrico a una distancia $d$ de una carga $Q$.
$\Delta V = \dfrac{\Delta E_{pe}}{|Q|}$ -> Definición de diferencia de potencial eléctrico: relaciona el trabajo o energía potencial con la carga.
$\Delta E_{pe} = |Q| \cdot |E| \cdot |\Delta x|$ -> Variación de energía potencial eléctrica: para un campo eléctrico uniforme y un desplazamiento $\Delta x$.
$\Delta V = |E| \cdot |\Delta x|$ -> Relación entre campo eléctrico y diferencia de potencial en un campo uniforme
Capacitores:
$C = \dfrac{Q}{\Delta V}$ -> Definición de capacidad eléctrica: relaciona la carga almacenada con la diferencia de potencial aplicada.
$C = \dfrac{\varepsilon_0 \cdot \varepsilon_r \cdot A}{d}$ -> Capacidad de un capacitor plano: depende del área de las placas, su separación y el material entre ellas.
$U = \dfrac{1}{2} \cdot C \cdot \Delta V^2 = \dfrac{1}{2} \cdot Q \cdot \Delta V = \dfrac{1}{2} \cdot \dfrac{Q^2}{C}$ -> Energía almacenada en un capacitor cargado: se puede expresar en función de $C$, $Q$ o $\Delta V$.
$\sigma = \dfrac{Q}{A}$ -> Densidad superficial de carga: carga por unidad de área en una de las placas del capacitor.
Corriente continua:
$I = \dfrac{Q}{\Delta t}$
$I = \dfrac{\Delta V}{R}$ -> Ley de Ohm
$R = \dfrac{\rho \cdot L}{A}$
$\text{Pot} = \Delta V \cdot I = I^2 \cdot R = \dfrac{\Delta V^2}{R}$
Resistencias en serie:
$R_T = R_1 + R_2 + \cdots$
$I_T = I_1 = I_2 = \cdots$
$\Delta V_T = \Delta V_1 + \cdots$
Resistencias en paralelo:
$\dfrac{1}{R_T} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + \cdots$
$I_T = I_1 + I_2 + \cdots$
$\Delta V_T = \Delta V_1 = \cdots$
 Profe: Juli
Profe: Juli